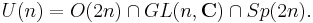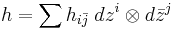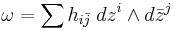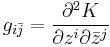Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure (a U(n)-structure) satisfying an integrability condition. In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.
This threefold structure corresponds to the presentation of the unitary group as an intersection:
Without any integrability conditions, the analogous notion is an almost Hermitian manifold. If the Sp-structure is integrable (but the complex structure need not be), the notion is an almost Kähler manifold; if the complex structure is integrable (but the Sp-structure need not be), the notion is a Hermitian manifold.
Kähler manifolds are named after the mathematician Erich Kähler and are important in algebraic geometry: they are a differential geometric generalization of complex algebraic varieties.
Contents |
Definition
A manifold with a Hermitian metric is an almost Hermitian manifold; a Kähler manifold is a manifold with a Hermitian metric that satisfies an integrability condition, which has several equivalent formulations.
Kähler manifolds can be characterized in many ways: they are often defined as a complex manifold with an additional structure (or a symplectic manifold with an additional structure, or a Riemannian manifold with an additional structure).
One can summarize the connection between the three structures via 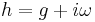 , where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structure, and
, where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structure, and  is the almost symplectic structure.
is the almost symplectic structure.
A Kähler metric on a complex manifold M is a hermitian metric on the tangent bundle 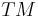 satisfying a condition that has several equivalent characterizations (the most geometric being that parallel transport induced by the metric gives rise to complex-linear mappings on the tangent spaces). In terms of local coordinates it is specified in this way: if
satisfying a condition that has several equivalent characterizations (the most geometric being that parallel transport induced by the metric gives rise to complex-linear mappings on the tangent spaces). In terms of local coordinates it is specified in this way: if
is the hermitian metric, then the associated Kähler form defined (up to a factor of i/2) by
is closed: that is, dω = 0. If M carries such a metric it is called a Kähler manifold.
The metric on a Kähler manifold locally satisfies
for some function K, called the Kähler potential.
A Kähler manifold, the associated Kähler form and metric are called Kähler-Einstein (or sometimes Einstein-Kähler) iff its Ricci tensor is proportional to the metric tensor, 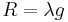 , for some constant λ. This name is a reminder of Einstein's considerations about the cosmological constant. See the article on Einstein manifolds for more details.
, for some constant λ. This name is a reminder of Einstein's considerations about the cosmological constant. See the article on Einstein manifolds for more details.
Examples
- Complex Euclidean space Cn with the standard Hermitian metric is a Kähler manifold.
- A torus Cn/Λ (Λ a full lattice) inherits a flat metric from the Euclidean metric on Cn, and is therefore a compact Kähler manifold.
- Every Riemannian metric on a Riemann surface is Kähler, since the condition for ω to be closed is trivial in 2 (real) dimensions.
- Complex projective space CPn admits a homogeneous Kähler metric, the Fubini-Study metric. An Hermitian form in (the vector space) Cn + 1 defines a unitary subgroup U(n + 1) in GL(n + 1,C); a Fubini-Study metric is determined up to homothety (overall scaling) by invariance under such a U(n + 1) action. By elementary linear algebra, any two Fubini-Study metrics are isometric under a projective automorphism of CPn, so it is common to speak of "the" Fubini-Study metric.
- The induced metric on a complex submanifold of a Kähler manifold is Kähler. In particular, any Stein manifold (embedded in Cn) or projective algebraic variety (embedded in CPn) is of Kähler type. This is fundamental to their analytic theory.
- The unit complex ball Bn admits a Kähler metric called the Bergman metric which has constant holomorphic sectional curvature.
- Every K3 surface is Kähler (by a theorem of Y.-T. Siu).
An important subclass of Kähler manifolds are Calabi–Yau manifolds.
Properties
(Deligne et al. 1975) showed that all Massey products vanish on a Kähler manifold. Manifolds with such vanishing are formal: their real homotopy type follows ("formally") from their real cohomology ring.
See also
- Almost complex manifold
- Hyper-Kähler manifold
- Kähler–Einstein metric
- Quaternion-Kähler manifold
- Complex Poisson manifold
References
- Deligne, P.; Griffiths, Ph.; Morgan, J.; Sullivan, D., (1975), "Real homotopy theory of Kähler manifolds", Invent. Math. 29: 245–274, doi:10.1007/BF01389853
- Alan Huckleberry and Tilman Wurzbacher, eds. Infinite Dimensional Kähler Manifolds (2001), Birkhauser Verlag, Basel ISBN 3-7643-6602-8.
- Andrei Moroianu, Lectures on Kähler Geometry (2007), London Mathematical Society Student Texts 69, Cambridge ISBN 978-0-521-68897-0.
- André Weil, Introduction à l'étude des variétés kählériennes (1958)